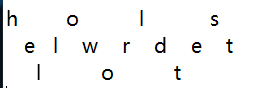攻防世界 —— Crypto(新手区)

发表于 | 分类于 | | 热度: ℃
字数统计: 4,943 | 阅读时长 ≈ 21

0x00 前言

最近打算边上课边刷一下攻防世界的题目，一是为了保持密码学的做题手感，二是为了打发上某些课的时间（指一心二用，因为某些课实在是太无聊了），话不多说，开始。

0x01 base64

解题思路

本题属于密码学部分的签到题，结合提示与附件内容可以发现其为base64加密，直接写脚本解密即可。

需要注意的是，python2中base系列直接对字符串进行加解密，得到的结果都是字符串类型。

然而python3中，如果直接对字符串类型的明文进行加密，系统会抛出类型错误报错：

base2.PNG-4kB

根据报错提示可知，python3中base系列函数对字节类型的变量而非字符串进行加解密，所以我们需要使用string.encode()函数完成string类型到bytes类型的转换，使用byte.decode()完成bytes类型到string类型的转换。

解题脚本

1
2
3
4
import base64
ciphertext = 'Y3liZXJwZWFjZXtXZWxjb21lX3RvX25ld19Xb3JsZCF9'
plaintext = base64.b64decode(ciphertext)
print(plaintext.decode())

一些经验

分辨base系列典型的三种加密方式对应密文：

  • Base16：该编码使用16个ASCII可打印字符对任意字节数据进行编码，编码后的数据量是原数据的两倍。故编码结果范围为十六进制数字。
  • Base32：该编码使用32个可打印字符对任意字节数据进行编码，编码结果范围为字母A-Z和数字2-7，如果位数不够则使用=进行填充。
  • Base64：该编码使用64个可打印ASCII字符将任意字节序列编码成ASCII字符串，编码结果范围为字母A-Z，a-z，数字0-9以及字符+/，如果位数不够则使用=进行填充。

我们可以观察得到的密文结尾，一般以=结尾的密文大概率是base32/64加密的结果。

当然，一般题目不会简单到提供base加密后的密文，然后经过一次解密直接得到flag。大部分对于base系列加解密应用的题目可分为两种：一种是将base作为混淆的手段嵌入到加解密算法中，我们需要通过多种分析写出逆算法解得flag；还有一种是将base与web系列的题目结合，用于加密数据包中的信息。

除此之外还有一类仅由base系列构成的加密，即使用base16/32/64进行多次加密，这类题目我们需要编写循环，根据每次解得密文的特点来选择下次解密使用的算法。当然，base36/58/85等算法在各类题目中也层出不穷，当使用常用base算法无法解密密文时，可以考虑这些不常见的算法。

我们来探寻base系列算法的本质，baseN就是使用选定的N个ASCII可打印字符将任意字节数据编码成ASCII字符串，从而达到正常传输数据的目的。我们可以将其等价转换为N进制来理解。

0x02 Caesar

解题思路

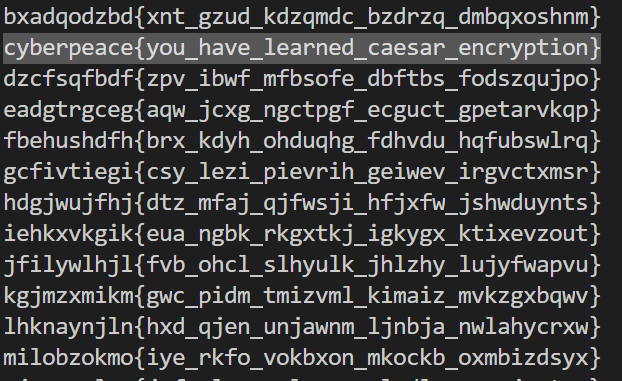
根据题目的提示Caesar，可知该题目解题的方法与凯撒密码相关。对于凯撒位移，我们直接采用爆破移动位数的方法，对于密文提供的{}和_这种特殊标志，我们保持原状即可。

最后从运行结果中找到合理的明文即为答案。

caesar.PNG-43.5kB

解题脚本

1
2
3
4
5
6
7
8
9
ciphertext = 'oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}'
for i in range(26):
    result = ''
    for item in ciphertext:
        if ord(item) > 122 or ord(item) < 97:
            result += item
        else:
            result += str(chr((ord(item)-ord('a')+i)%26 + ord('a')))
    print(result)

一些经验

原始的凯撒密码是一个移动位数为3的单表代换加密过程。由凯撒延申出来的ROT系列如ROT5，ROT13等将移动位数变成了5位和13位等。对于该系列的密文，我们可以进行爆破处理，从最终的结果中寻找合理的结果作为明文。还有一种名为雷劈密码的类凯撒加密，其特点为每一个字符移动的位数不同但有等差规律。

对于纯凯撒密码的题目，如果有flag格式，其移动位数可以通过{前的字符与flag前缀一一对应得到。

0x03 Morse

解题思路

本题的提示为Morse即摩斯电码，我们打开附件可以发现只有0和1两个字符，并且分隔符为空格。

使用python编写自动替代脚本先将1转换为.，0转换为-，进行解密测试，如果不正确则进行相反转换即可。

解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 摩斯电码检测
def Morse_decode(ciphertext):
    Morse_dict = {".-" : "A",
            "-..." : "B",
            "-.-." : "C",
            "-.." : "D",
            "." : "E",
            "..-." : "F",
            "--." : "G",
            "...." : "H",
            ".." : "I",
            ".---" : "J",
            "-.-" : "K",
            ".-.." : "L",
            "--" : "M",
            "-." : "N",
            "---" : "O",
            ".--." : "P",
            "--.-" : "Q",
            ".-." : "R",
            "..." : "S",
            "-" : "T",
            "..-" : "U",
            "...-" : "V",
            ".--" : "W",
            "-..-" : "X",
            "-.--" : "Y",
            "--.." : "Z",
            ".----" : "1",
            "..---" : "2",
            "...--" : "3",
            "....-" : "4",
            "....." : "5",
            "-...." : "6",
            "--..." : "7",
            "---.." : "8",
            "----." : "9",
            "-----" : "0",
            "..--.." : "?",
            "-..-." : "/",
            "-.--.-" : "()",
            "-....-" : "-",
            ".-.-.-" : "."
            }
    all_variable = list(set(ciphertext.replace(" ", "")))
    try:
        tmp_cipher = ciphertext.replace(all_variable[0], ".").replace(all_variable[1],"-").split(" ")
        final_result = ""
        for item in tmp_cipher:
            final_result += Morse_dict.get(item)
    except TypeError:
        tmp_cipher = ciphertext.replace(all_variable[0], "-").replace(all_variable[1],".").split(" ")
        final_result = ""
        for item in tmp_cipher:
            final_result += Morse_dict.get(item) 
    return final_result
if __name__ == "__main__":
    ciphertext = input("Please input the ciphertext:")
    plaintext = Morse_decode(ciphertext)
    print("The result is :\n" + plaintext + "\n" + plaintext.lower())

一些经验

如果题目给出的密文只包含两个字符并且有明显分割，可以考虑培根密码或者摩斯电码。不同的是培根密码每5个字符为一组加密单个字符，而摩斯电码每个码组长度不定。

0x04 混合编码

解题思路

根据题目的提示混合编码，我们将拿到的字符串先进行base64解码，得到HTML实体编码。将去掉特殊字符后的字符串分割并进行ASCII字符转换。转换后得到一串字符串：

混合编码.PNG-4.6kB

对该字符串再次进行base64解码，得到以/分割的一串数字，将该串分割之后转换为ASCII可读字符即为flag。

解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import base64
ciphertext = 'JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzk7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM2ODsmIzY5OyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjNTI7JiM3NjsmIzEyMjsmIzEwNzsmIzUzOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc3OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiMxMDc7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzg7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjODQ7JiM2OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzUwOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc4OyYjMTA1OyYjNTY7JiM1MzsmIzc4OyYjMTIxOyYjNTY7JiM1MzsmIzc5OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM5OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjNjk7JiMxMTk7JiM3NzsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjNjU7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM2OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjMTA3OyYjNTM7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM4NDsmIzEwNzsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzEyMDsmIzc2OyYjMTIyOyYjNjk7JiMxMjA7JiM3ODsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjMTAzOyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjMTE5Ow=='
plain1 = base64.b64decode(ciphertext)
# print(plain1)
plain2 = plain1.decode().replace(";", "").split("&#")
# print(plain2)
plain3 = ""
for item in plain2:
    if item == '':
        continue
    else:
        plain3 += chr(int(item))
# print(plain3)
plain4 = base64.b64decode(plain3).decode()
# print(plain4)
plain5 = plain4.split("/")
plain6 = ""
# print(plain5)
for item in plain5:
    if item == "":
        continue
    else:
        plain6 += chr(int(item))
print(plain6)

0x05 不仅仅是Morse

解题思路

该题目的附件显然是摩斯电码，我们编写脚本进行解密后发现有一串AB交替连缀的字符串，显然为培根密码。

不仅仅是Morse.PNG-13.4kB

编写对应脚本解码即可。

解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
# 摩斯电码检测
def Morse_decode(ciphertext):
    Morse_dict = {".-" : "A",
            "-..." : "B",
            "-.-." : "C",
            "-.." : "D",
            "." : "E",
            "..-." : "F",
            "--." : "G",
            "...." : "H",
            ".." : "I",
            ".---" : "J",
            "-.-" : "K",
            ".-.." : "L",
            "--" : "M",
            "-." : "N",
            "---" : "O",
            ".--." : "P",
            "--.-" : "Q",
            ".-." : "R",
            "..." : "S",
            "-" : "T",
            "..-" : "U",
            "...-" : "V",
            ".--" : "W",
            "-..-" : "X",
            "-.--" : "Y",
            "--.." : "Z",
            ".----" : "1",
            "..---" : "2",
            "...--" : "3",
            "....-" : "4",
            "....." : "5",
            "-...." : "6",
            "--..." : "7",
            "---.." : "8",
            "----." : "9",
            "-----" : "0",
            "..--.." : "?",
            "-..-." : "/",
            "-....-" : "-",
            ".-.-.-" : ".",
            "-.-.--" : "!",
            "-.--." : "(",
            ".--.-." : "@",
            "---..." : ":",
            "-...-" : "=",
            "-....-" : "-",
            "-.--.-" : ")",
            "--..--" : ",",
            ".----." : "'",
            "..--.-" : "_",
            "...-..-" : "$",
            "-.-.-." : ";",
            "-..-." : "/",
            ".-..-." : "\"",
            "...." : "&"
            }
    all_variable = list(set(ciphertext.replace("/", "")))
    print(all_variable)
    try:
        tmp_cipher = ciphertext.replace(all_variable[0], ".").replace(all_variable[1],"-").split("/")
        print(tmp_cipher)
        final_result = ""
        for item in tmp_cipher:
            final_result += Morse_dict.get(item)
    except TypeError:
        tmp_cipher = ciphertext.replace(all_variable[0], "-").replace(all_variable[1],".").split("/")
        final_result = ""
        for item in tmp_cipher:
            final_result += Morse_dict.get(item) 
    return final_result
def Bacon_decode(ciphertext):
    Bacon_dict = {
        "aaaaa" : "A",
        "aaaab" : "B",
        "aaaba" : "C",
        "aaabb" : "D",
        "aabaa" : "E",
        "aabab" : "F",
        "aabba" : "G",
        "aabbb" : "H",
        "abaaa" : "I",
        "abaab" : "J",
        "ababa" : "K",
        "ababb" : "L",
        "abbaa" : "M",
        "abbab" : "N",
        "abbba" : "O",
        "abbbb" : "P",
        "baaaa" : "Q",
        "baaab" : "R",
        "baaba" : "S",
        "baabb" : "T",
        "babaa" : "U",
        "babab" : "V",
        "babba" : "W",
        "babbb" : "X",
        "bbaaa" : "Y",
        "bbaab" : "Z"
    }
    final_plain = ""
    for i in range(0, len(ciphertext), 5):
        final_plain += Bacon_dict.get(ciphertext.lower()[i:i+5])
    return final_plain
def main():
    ciphertext = input("Please input the ciphertext:")
    plaintext = Morse_decode(ciphertext)
    plaintext = plaintext[30:]
    final_plain = Bacon_decode(plaintext)
    print(final_plain)
    print(final_plain.lower())


if __name__ == "__main__":
    main()

0x06 幂数加密

解题思路

根据题目提示百度一下二进制幂数加密，其原理为十进制数都可以用二进制幂的形式表示，并且可以用十进制数字表示字符偏离首字母A的距离，于是我们可以用二进制幂来加密英文字符串。编写脚本解题即可。

解题脚本

1
2
3
4
5
6
7
8
9
ciphertext = '8842101220480224404014224202480122'
ciphertext = ciphertext.split('0')
plaintext = ""
for item in ciphertext:
    tmp = 0
    for var in item:
        tmp += eval(var)
    plaintext += chr(64 + tmp)
print(plaintext)

0x07 Railfence

解题思路

根据提示可知为railfence即栅栏密码。下载附件后观察密文：

1
ccehgyaefnpeoobe{lcirg}epriec_ora_g

由于题目的flag前缀为cyberpeace，但密文中这十个字母的间距不相等，而栅栏密码应用了等间距分组的思想，显然本题目不是普通的定间距栅栏密码。

多方搜寻后发现栅栏密码存在W形式的变种，举例如下：

明文为helloworldtest，key=3时，结果为：

railfence1.PNG-1.5kB

加密结果为holselwrdetlot。

回到本题，其实可以根据第一个字符c和第二个字符y之间的距离为4并且总字符数为35推测出第一行两字母之间相距7个字符，从而可以得到key=5，还原之后得到flag。

railfence2.PNG-3.2kB

对于W型的栅栏密码，有专门的解密网址：W型栅栏密码

一些经验

CTF密码学题目中，对古典密码的考察较少；如果需要对其进行考察，则大概率会考察其变体。当使用常规古典密码解法无法得到合理的flag时，考虑复制粘贴密文并Google或百度，兴许可以发现新姿势。平时需要积累一些奇奇怪怪的网站，关键时刻或许可以派上用场（指做题。

0x08 easy_RSA

解题思路

该题目不能称作基本的RSA解密，最多只是一个求RSA中特定参数的过程。题目给出了p，q和e，求解密指数d。RSA原理中有：

phi(n) = (p-1) * (q-1)

e * d ≡ 1 (mod phi(n))

直接编写脚本计算即可。

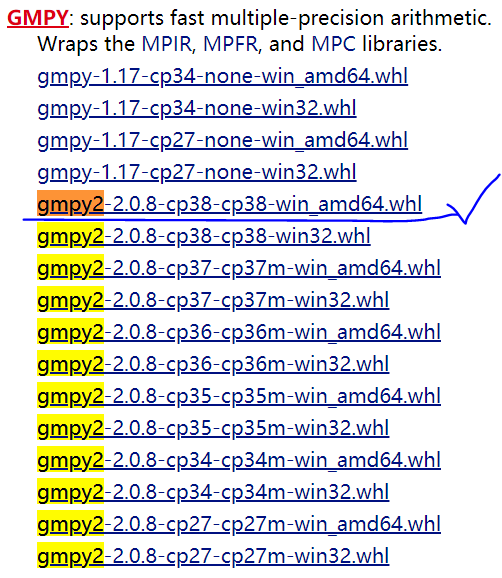
由于新的python环境没有安装解题需要的gmpy2库，于是考虑手动安装，python版本为3.8。命令行中直接输入pip install gmpy2瞬间满屏都是红色报错，仔细审查后发现出错的核心为Failed building wheel for gmpy2即缺少gmpy2对应的wheel文件。于是直接pip install wheel安装wheel库，然后从python扩展wheel文件网站中下载对应的wheel文件即可。下载之后在cmd中输入pip install + gmpy2.wheel文件绝对路径即可完成安装。

gmpy2.PNG-41.3kB

解题脚本

1
2
3
4
5
6
7
import gmpy2
p=473398607161
q=4511491
e=17
phi = (p-1)*(q-1)
d = gmpy2.invert(e, phi)
print(d)

0x09 easychallenge

解题思路

本题目提供了将python脚本编译后的pyc文件。下载附件后使用uncompyle6 xxx.pyc > xx.py命令将其反编译为python文件，可以获得加密脚本的细节如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import base64
def encode1(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x + 25
        s += chr(x)
    return s
def encode2(ans):
    s = ''
    for i in ans:
        x = ord(i) + 36
        x = x ^ 36
        s += chr(x)
    return s
def encode3(ans):
    return base64.b32encode(ans)
flag = ' '
print 'Please Input your flag:'
flag = raw_input()
final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
if encode3(encode2(encode1(flag))) == final:
    print 'correct'
else:
    print 'wrong'

编写解密脚本后发现嵌套解密过程中出现问题：

ezchallenge1.PNG-5.6kB

ezchallenge.PNG-5kB

显然使用utf-8编码无法对结果进行解码。为了检测base解密结果为何种编码，引入chardet库，使用pip安装并导入后检测decode3()函数解密结果的编码类型，并使用该编码类型进行正确解码。（chardet.detect()函数返回结果为字典类型，故使用索引）

1
2
3
4
5
6
import chardet
plain_tmp = decode3(ciphertext)
code = chardet.detect(plain_tmp)
# code : {'encoding' : 'ISO-8859-1','cofidence' : 0.73, 'language' : ''}
final_code = code['encoding']
flag = decode1(decode2(decode3(plain_tmp).decode(final_code)))

解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import base64
import chardet
def decode3(ciphertext):
    return base64.b32decode(ciphertext)

def decode2(ciphertext):
    plain2 = ''
    for item in ciphertext:
        x = ord(item) ^ 36
        x = x - 36
        plain2 += chr(x)
    return plain2
def decode1(ciphertext):
    plain1 = ''
    for item in ciphertext:
        x = ord(item) - 25
        x = x ^ 36
        plain1 += chr(x)
    return plain1
if __name__ == "__main__":
    ciphertext = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
    plain_tmp = decode3(ciphertext)
    code = chardet.detect(plain_tmp)
    final_code = code['encoding']
    flag = decode1(decode2(plain_tmp.decode(final_code)))
    print(flag)

0x0A Normal_RSA

解题思路

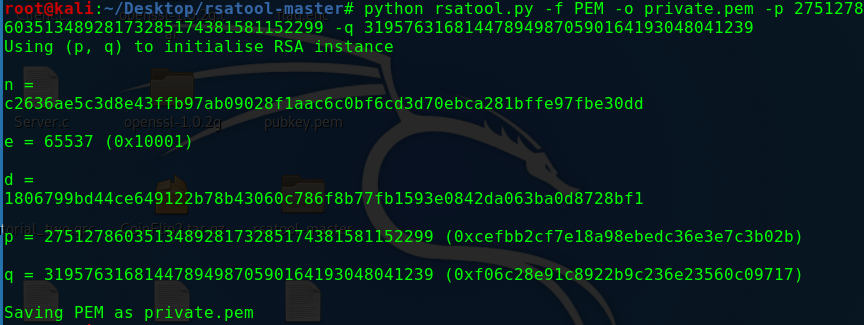
下载附件并解压，打开后发现给出了flag.enc和pub.key这两个文件。根据文件后缀得知本题显然为文件类型RSA题目。我们下载rsatool-master并向其提供p和q的值以生成private.pem解密证书。

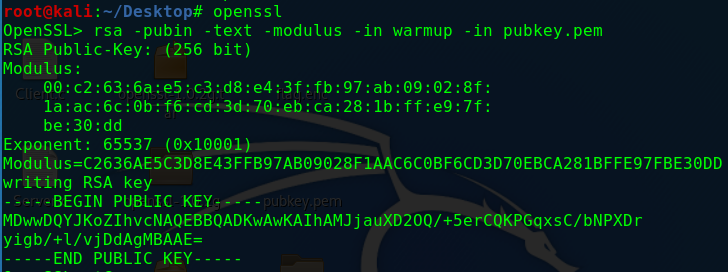
将题目提供的文件拖入kali虚拟机，使用其自带的openssl功能从公钥文件pubkey.pem中获得模数N和加密指数e：

normal_RSA.PNG-114.9kB

可以看到Modulus的十六进制表示，将其转换为十进制并进行大数分解得到p和q，这里推荐一个大数分解的网站：factordb.com。分解之后进入rsatool-master的目录，执行如下命令生成私钥文件：

normal_RSA2.PNG-150.2kB

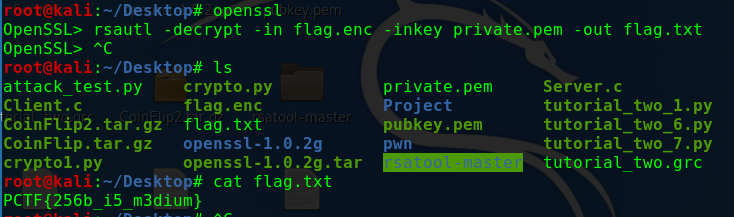
得到私钥文件之后使用openssl命令解密可得flag：

normal_RSA3.PNG-99.1kB

0x0B 转轮机加密

解题思路

根据提示搜索托马斯杰斐逊转轮机密码，可以找到其加解密原理，我们结合题目给出的密码表和密文进行简要说明。

转轮机.PNG-34.7kB

可以看到，题目给出具有标号的密码表，我们按照所给的密钥对密码表进行行序交换。对于交换后的结果，将密码本的每行与密文的每个字母对应，使对应行的首字母为密文的对应字母即可。

例如将第二行KPBELNACZDTRXMJQOYHGVSFUWI移动到第一行并变成NACZDTRXMJQOYHGVSFUWIKPBEL。最后将排序好的字母表以列为单位输出，从中寻找语法正确的明文即可。

（本题flag没有前缀，得到的字符串直接变成小写输入即可！

解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
key = [2,3,7,5,13,12,9,1,8,10,4,11,6]
ciphertext = 'NFQKSEVOQOFNP'
tmp_alphabet = []
final_alphabet = []
new_alphabet = []
# 对输入的密码表按照密钥进行行排序
f = open('test.txt', 'r')
for line in f:
    tmp_alphabet.append(line.strip('< ').strip('\n').strip(' <'))
for item in key:
    final_alphabet.append(tmp_alphabet[item - 1])
for i in range(len(ciphertext)):
    baffle = final_alphabet[i].index(ciphertext[i])
    new_alphabet.append(final_alphabet[i][baffle:] + final_alphabet[i][:baffle])
for j in range(len(new_alphabet[0])):
    plaintext = ''
    for item in new_alphabet:
        plaintext += item[j]
    print(plaintext.lower())

0x0C easy_ECC

解题思路

本题主要考察了基于椭圆曲线离散对数困难问题（即ECC）的加密签名过程中公钥的获取过程。下面先对椭圆曲线相关知识进行简要介绍。

椭圆曲线定义

首先来看椭圆曲线的定义，椭圆曲线标准公式为：

其中$4a^3 + 27b^2 ≠ 0$这个限定条件保证曲线不包含奇点（即无穷远点）。这种椭圆曲线被称为Weierstrass标准形式。当然，为了完整定义椭圆曲线，还需要一个无穷远点作为曲线的一部分，这里使用A表示。

最终可以将表达式精炼为：

对于生成元P，其加法是一个闭环，nP的集合是椭圆曲线形成的群里的一个具有循环性质的子群，根据此i性质可以简化nP的代码。

ECC算法步骤

将ECC算法步骤总结如下：

  • 计算椭圆曲线的阶N
  • 选择一个阶为n的子群，n为素数且为N的因子
  • 计算辅因子h = N/n
  • 在曲线上选择一个基点P
  • 计算G = hP
  • 如果G是0，那么重新选择基点，否则找到了阶为n，生成元为P的子群

困难问题本质

现在假设有一条在有限域$F_{p}$上的椭圆曲线，要解决的困难问题如下：

已知P和Q的情况下，对于Q=k*P，如何计算满足要求的k?

这个就是椭圆曲线中的离散对数问题。

ECDH

进行加解密之前，我们首先选取一些重要的域参数：

  • 素数p
  • 椭圆曲线系数a与b
  • 基点（生成元）G
  • 子群的阶n
  • 辅因子h

之后将这六个域参数合成一个六元组（p,a,b,G,n,h）

选取完毕一个六元组后，定义如下内容：

  • 私钥：一个随机的整数d，选取自{1,2,3,…..,n-1}
  • 公钥：H = dG（G是循环子群的生成元）

如果我们已知d与六元组，计算出H是一件非常简单的事情（也就是本题目需要解决的问题）。但是如果我们只知道H和G，去寻找符合要求的d是非常困难的，这就是上面提到的离散对数问题。

下面对ECDH算法进行说明，该算法流程基于DH密钥交换协议

  • Alice和Bob首先约定一个六元组，生成自己的私钥和公钥，定义关键参数如下：
    • Alice Private Key: $d_{A}$
    • Alice Public Key: $H{A} = d{A}*G$
    • Bob Private Key: $d_{B}$
    • Bob Public Key:$H{B} = d{B}*G$
  • Alice和Bob公开交换公钥，第三方可以窃听到$H{A}$和$H{B}$，但由于困难问题的存在，其无法解出$d{A}$和$d{B}$
  • Alice用自己的私钥计算$S{A} = d{A}H{B}$，Bob用自己的私钥计算$S{B} = d_{B}H_{A}$

由于$S = d{A}*H{B} = d{A}(d{B}G) = d{B}(d{A}G)$，显然$S{A} = S{B}$。基于以上步骤，Alice和Bob完成了DH密钥交换，他们可以将该密钥用于对称密码如AES中来传递信息。

ECDSA

接下来简单介绍一下ECDSA原理。

在预定完毕一个六元组后，Alice定义公钥和私钥：

  • 私钥：一个选自[1,n-1]范围内的随机整数$d_{A}$
  • 公钥：$H{A} = d{A}*G$，其中G是循环子群的生成元

随后，Alice进行如下操作：

  • 从[1,n-1]范围内选取一个随机的整数k
  • 计算$P = k*G$
  • 计算$r \equiv x{p} (mod n)$，其中$x{p}$是P的横坐标
  • 如果r = 0则重新选取k
  • 计算$s \equiv k^{-1}(z+rd{A}) (mod n)$，其中$d{A}$是Alice的私钥，$k^{-1}$是k的逆元
  • 如果s = 0则重新选取k
  • 将(r, s)封装为一个签名

需要注意的是，私钥必须为素数，否则在计算模逆的时候会出现一些奇奇怪怪的状况，直接导致ECDSA无法正常使用。

对于Bob，其拿到Alice传递的信息z和Alice的签名(r, s)，通过以下方法对签名进行验证：

  • 计算$u_{1} \equiv s^{-1}*z (mod n)$
  • 计算$u_{2} \equiv s^{-1}*r (mod n)$
  • 计算$P{0} = u{1}G + u_{2}H_{A}$
  • 当且仅当$r \equiv x{p}(mod n) $的时候$P{0} = H_{A}$

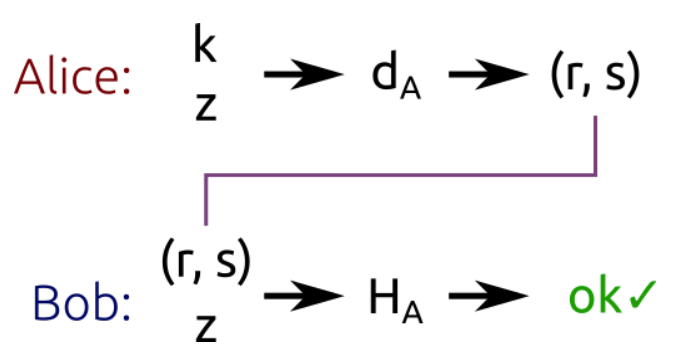
可以将ECDSA的过程用下图进行概括：

ECDSA.PNG-32.2kB

回到题目，本题给出p，a，b和生成元G以及私钥k，要求公钥。即求K(x, y) = k*G，最后返回x+y的值作为flag。

关于ECC原理及攻击方法，可以参考ShaoBaoBaoR师傅的博客，其中有三篇ECC相关文章分析地非常透彻：

解题脚本

相关代码参考上面提到师傅文章中给出的Github项目：shaobaobaoer的椭圆曲线密码学习之路，代码逻辑非常清晰易懂。

请作者吃个小鱼饼干吧
分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多